线性回归

线性回归

本模块将介绍线性回归概念。

学习目标：

• 解释损失函数及其运作方式。
• 定义并描述梯度下降如何找到最佳模型参数。
• 介绍如何调整超参数以高效训练线性模型。

前提条件： 本模块假定您熟悉以下模块中介绍的概念：

• 机器学习简介

线性回归是一种用于查找变量之间关系的统计技术。 在机器学习背景下，线性回归用于查找特征与标签之间的关系。

例如，假设我们想根据汽车的重量预测汽车的燃油效率（以每加仑英里数表示），并且我们有以下数据集：

以千为单位的英镑（特征）	每加仑燃油行驶的英里数 （标签）
3.5	18
3.69	15
3.44	18
3.43	16
4.34	15
4.42	14
2.37	24

如果我们绘制这些点，会得到以下图表：

图 1. 汽车重量（以磅为单位）与每加仑汽油能行驶的英里数评级。汽车越重，每加仑燃油行驶里程数通常越低。

我们可以通过在这些点之间绘制最佳拟合线来创建自己的模型：

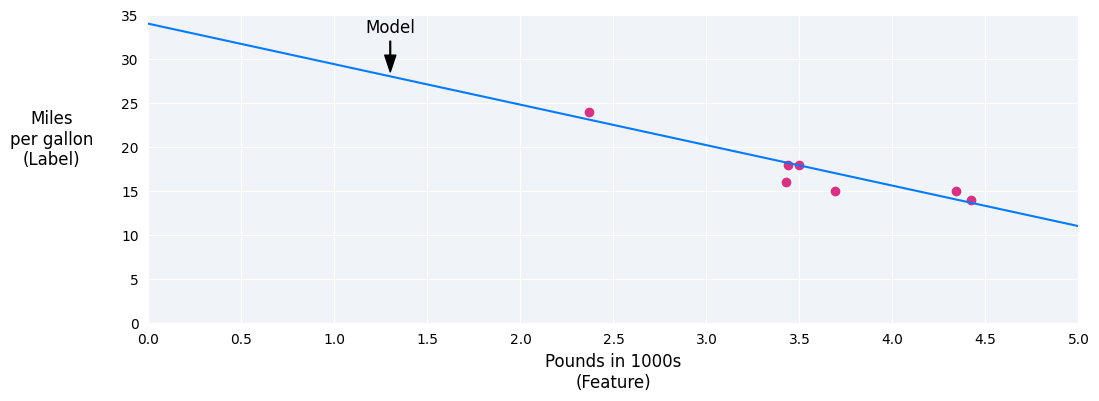
图 2. 通过上图数据绘制的最佳拟合线。

线性回归方程

用代数术语来说，该模型可定义为 $y=mx+b$，其中

• $y$ 是每加仑燃油行驶里程数，即我们要预测的值。
• $m$ 是直线的斜率。
• $x$ 是磅，即我们的输入值。
• $b$ 是 y 轴截距。

在机器学习中，线性回归模型的方程式如下所示：

$$y^{\prime }=b+w_1{x}_1$$

其中：

• $y^{\prime }$ 是预测标签（输出）。
• $b$ 是模型的偏差。偏差与直线代数方程式中的 y 轴截距概念相同。在机器学习中，偏差有时称为 $w_0$。偏差是模型的形参，在训练期间计算得出。
• $w_1$ 是特征的权重。权重与线性代数方程式中的斜率 $m$ 的概念相同。权重是模型的形参，在训练期间计算得出。
• $x_1$ 是一个特征，即输入。

在训练期间，模型会计算出可生成最佳模型的权重和偏差。

图 3. 线性模型的数学表示法。

在我们的示例中，我们将根据绘制的直线计算权重和偏差。偏差为 34（直线与 y 轴的交点），权重为 -4.6（直线的斜率）。该模型可定义为 $y^{\prime }=34+(-4.6)(x_1)$，我们可以使用它进行预测。例如，使用此模型，一辆 4,000 磅的汽车的预测燃油效率为每加仑 15.6 英里。

图 4. 根据该模型，一辆 4,000 磅的汽车的预测燃油效率为每加仑 15.6 英里。

具有多种特征的模型

虽然本部分中的示例仅使用一项特征（汽车的重量），但更复杂的模型可能依赖于多项特征，每项特征都有一个单独的权重（$w_1$、$w_2$ 等）。例如，依赖于 5 个特征的模型可以写成如下形式：

$y^{\prime }=b+w_1{x}_1+w_2{x}_2+w_3{x}_3+w_4{x}_4+w_5{x}_5$

例如，预测燃油效率的模型还可以使用以下特征：

• 发动机排量
• 加速
• 气缸数
• 马力

此模型可写为：

图 5. 一个包含 5 个特征的模型，用于预测汽车的每加仑燃油行驶里程评级。

通过绘制这几个额外特征的图表，我们可以看到它们与标签（每加仑英里数）也存在线性关系：

图 6. 汽车的排量（以立方厘米为单位）及其每加仑行驶里程数评级。一般来说，汽车的发动机越大，每加仑燃油行驶里程数就越低。

图 7. 汽车的加速度和每加仑燃油行驶里程数评级。汽车的加速时间越长，每加仑燃油行驶里程数通常越高。

练习：检查您的理解情况

在训练期间，线性回归方程的哪些部分会更新？

• 预测
• 偏差和权重
• 特征值

说明： 在训练期间，模型会更新偏差和权重。 特征值是数据集的一部分，因此在训练期间不会更新。 预测结果不是在训练期间更新的。

**关键术语**

• 偏差
• 功能
• 标签
• 线性回归
• 参数
• 权重

线性回归：损失函数

损失是一个数值指标，用于描述模型的预测有多么不准确。损失用于衡量模型预测与实际标签之间的差距。训练模型的目标是尽可能降低损失，使其达到最低值。

在下图中，您可以将损失直观地表示为从数据点到模型的箭头。箭头显示了模型的预测与实际值之间的差距。

图 8. 损失是从实际值到预测值进行衡量的。

损失距离

在统计学和机器学习中，损失用于衡量预测值与实际值之间的差异。损失侧重于值之间的距离，而不是方向。例如，如果模型预测值为 2，但实际值为 5，我们并不关心损失为负值（$2-5=-3$）。相反，我们关心的是这两个值之间的距离为 $3$。因此，所有计算损失的方法都会移除符号。

以下是两种最常见的去除符号的方法：

• 计算实际值与预测值之差的绝对值。
• 计算实际值与预测值之差的平方。

损失类型

在线性回归中，有四种主要类型的损失，如下表所示。

损失类型	定义	公式
$L_1$ 损失	预测值与实际值之间的差的绝对值之和。	$∑
平均绝对误差 (MAE)	一组 N 个示例的平均 $L_1$ 损失。	$\frac{1}{N} ∑
$L_2$ 损失	预测值与实际值之间的平方差之和。	$\sum (\mathrm{实}\mathrm{际}\mathrm{值}-\mathrm{预}\mathrm{测}\mathrm{值}{)}^2$
均方误差 (MSE)	一组 N 个示例的平均 $L_2$ 损失。	$\frac{1}{N}\sum (\mathrm{实}\mathrm{际}\mathrm{值}-\mathrm{预}\mathrm{测}\mathrm{值}{)}^2$

$L_1$ 损失与 $L_2$ 损失（或 MAE 与 MSE）之间的功能差异在于平方。当预测值与标签之间的差值较大时，平方运算会使损失变得更大。当差值较小时（小于 1），平方运算会使损失更小。

在同时处理多个示例时，我们建议对所有示例的损失求平均值，无论使用 MAE 还是 MSE。

损失计算示例

使用之前的最佳拟合线，我们将计算单个示例的 $L_2$ 损失。根据最佳拟合线，我们得出以下权重和偏差值：

• 权重：$-4.6$
• 偏差: $34$

如果模型预测一辆 2,370 磅的汽车每加仑汽油能行驶 23.1 英里，但实际上该汽车每加仑汽油能行驶 26 英里，那么我们计算 $L_2$ 损失的方式如下：

注意： 该公式使用 2.37，因为图表按千磅为单位进行缩放

值	公式	结果
预测	$\mathrm{偏}\mathrm{差}+(\mathrm{权}\mathrm{重}\ast \mathrm{特}\mathrm{征}\mathrm{值})$ $34+(-4.6\ast 2.37)$	$23.1$
实际值	$label$	$26$
$L_2$ 损失	$(\mathrm{实}\mathrm{际}\mathrm{值}-\mathrm{预}\mathrm{测}\mathrm{值}{)}^2$ $(26-23.1{)}^2$	$8.41$

在本例中，相应单个数据点的 $L_2$ 损失为 8.41。

选择损失

是否使用 MAE 或 MSE 可能取决于数据集以及您希望如何处理某些预测。数据集中的大多数特征值通常都位于一个明显的范围内。例如，汽车的重量通常介于 2,000 磅到 5,000 磅之间，每加仑汽油可行驶的里程介于 8 英里到 50 英里之间。一辆 8,000 磅的汽车或一辆每加仑汽油能行驶 100 英里的汽车都超出了典型范围，会被视为离群点。

离群值还可以指模型的预测值与实际值之间的差距。例如，3,000 磅在典型汽车重量范围内，而每加仑 40 英里在典型燃油效率范围内。不过，如果一辆 3,000 磅的汽车每加仑汽油能行驶 40 英里，那么就模型的预测而言，这辆汽车将是一个离群点，因为模型会预测一辆 3,000 磅的汽车每加仑汽油能行驶大约 20 英里。

选择最佳损失函数时，请考虑您希望模型如何处理离群值。例如，MSE 会使模型更接近离群值，而 MAE 则不会。与 $L_1$ 损失相比，$L_2$ 损失对离群值的罚分要高得多。例如，以下图片展示了使用 MAE 训练的模型和使用 MSE 训练的模型。红线表示将用于进行预测的完全训练的模型。与使用 MAE 训练的模型相比，离群点更接近使用 MSE 训练的模型。

图 9. 使用 MSE 训练的模型会更接近离群值。

图 10. 使用 MAE 训练的模型离离群值更远。

请注意模型与数据之间的关系：

• MSE。模型更接近离群值，但距离大多数其他数据点更远。
• MAE。模型离离群点的距离更远，但离大多数其他数据点的距离更近。

点击相应图标可查看有关选择损失指标的更多指南

选择 MSE：

• 如果您想严厉惩罚大误差。
• 如果您认为离群值很重要，并且表明模型应考虑的真实数据方差。

注意：MSE 的数学属性通常会使优化更顺畅。均方根误差 (RMSE) 通常用于将误差恢复为与标签相同的单位。

选择 MAE：

• 如果您的数据集中存在您不希望对模型产生过大影响的显著离群值。MAE 更稳健。
• 如果您希望损失函数能更直接地解释为平均误差幅度。

实际上，您选择的指标还可能取决于具体的业务问题以及哪种类型的错误成本更高。

检查您的理解情况

请看以下两个图，它们显示了线性模型对数据集的拟合情况：

在对曲线图中绘制的数据点进行评估时，哪个线性模型的均方误差 (MSE) 较高？

• 左侧的模型。

  该行上的六个示例的总损失为 0。不在直线上的四个示例与直线的偏差并不大，因此即使对它们的偏移量进行平方处理，仍会得到较低的值：$MSE=\frac{0^2+1^2+0^2+1^2+0^2+1^2+0^2+1^2+0^2+0^2}{10}=0.4$

• 右侧的模型。

  该行上的 8 个示例的总损失为 0。不过，尽管只有两个点在线外，但这两个点离线的距离依然是左图中离群点的 2 倍。平方损失进一步加大差异，因此两个单位的偏移量产生的损失是一个单位的 4 倍：$MSE=\frac{0^2+0^2+0^2+2^2+0^2+0^2+0^2+2^2+0^2+0^2}{10}=0.8$

**关键术语**

• 平均绝对误差 (MAE)
• 均方误差 (MSE)
• $L_1$
• $L_2$
• 损失
• 离群值
• 预测

线性回归：梯度下降

梯度下降法是一种数学技巧，可迭代地找到能使模型产生最低损失的权重和偏差。梯度下降法通过重复以下过程（迭代次数由用户定义）来找到最佳权重和偏差。

模型开始训练时，权重和偏差会随机化为接近于零的值，然后重复执行以下步骤：

1. 使用当前权重和偏差计算损失。
2. 确定可减少损失的权重和偏差的移动方向。
3. 将权重和偏差值沿可减少损失的方向移动少量距离。
4. 返回到第 1 步，重复该过程，直到模型无法进一步减少损失为止。

下图概述了梯度下降法为找到可生成损失最低的模型的权重和偏差而执行的迭代步骤。

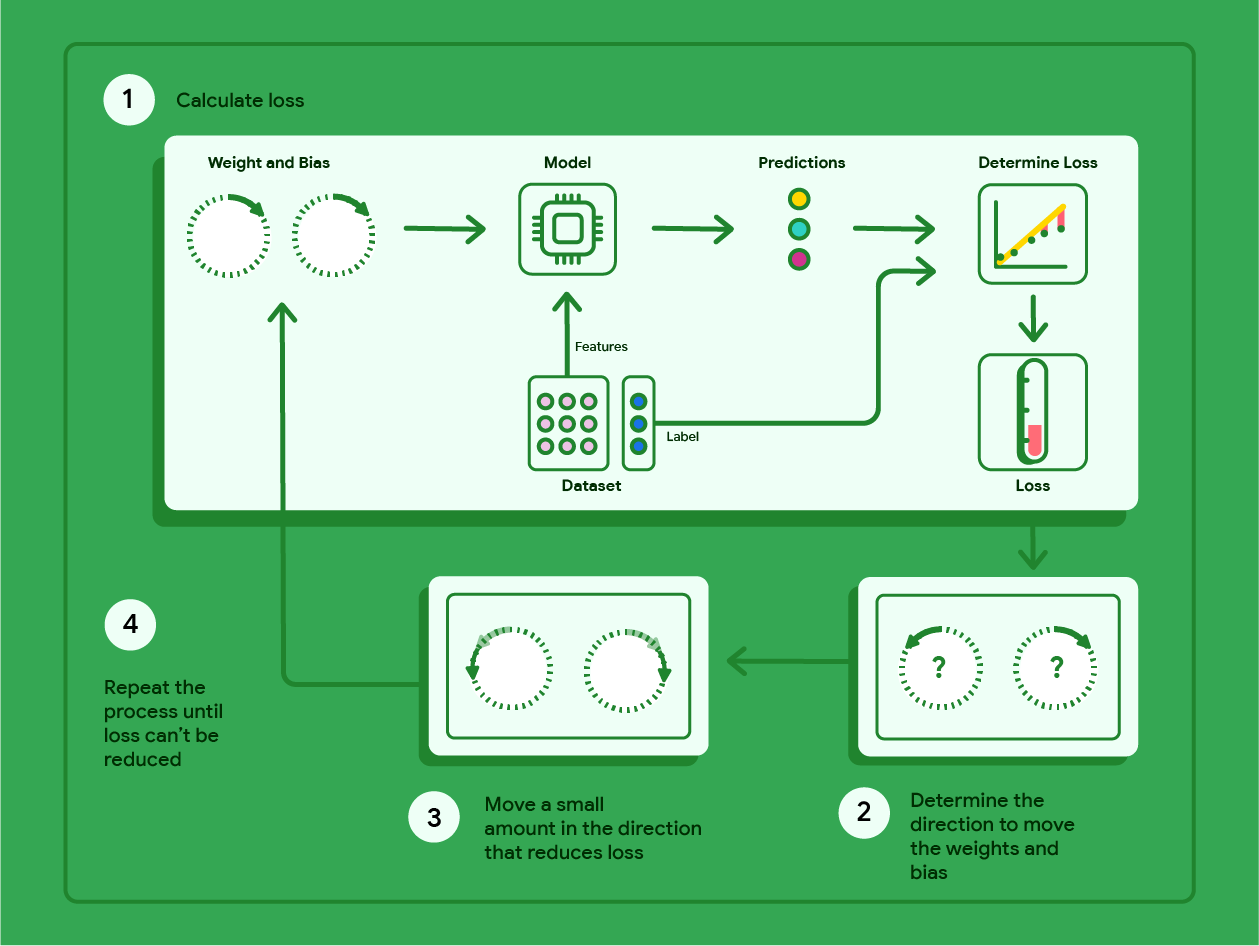
图 11. 梯度下降是一种迭代过程，用于找到可使模型产生最低损失的权重和偏差。

点击加号图标，详细了解梯度下降背后的数学原理。

在具体层面上，我们可以使用一个小数据集（包含 7 个示例，分别表示汽车的重量（以磅为单位）和每加仑燃油行驶里程数）来逐步完成梯度下降：

以千为单位的英镑（特征）	每加仑燃油行驶的英里数（标签）
3.5	18
3.69	15
3.44	18
3.43	16
4.34	15
4.42	14
2.37	24

1. 模型通过将权重和偏差设置为零来开始训练：$$Weight:0$$$$Bias:0$$$$y=0+0(x_1)$$
2. 使用当前模型参数计算 MSE 损失：$$Loss=\frac{(18-0{)}^2+(15-0{)}^2+(18-0{)}^2+(16-0{)}^2+(15-0{)}^2+(14-0{)}^2+(24-0{)}^2}{7}$$$$Loss=303.71$$
3. 计算每个权重和偏置处损失函数切线的斜率：$$Weightslope:-119.7$$$$Biasslope:-34.3$$
   点击了解如何计算斜率。

   为了获得与权重和偏差相切的直线的斜率，我们对损失函数相对于权重和偏差求导，然后求解方程。

   我们将预测方程写为：
   $f_{w,b}(x) = (w*x)+b$。

   我们将实际值写为：$y$。

   我们将使用以下公式计算 MSE：
   $$\frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2$$
   其中，$i$ 表示第 $i$ 个训练样本，$M$ 表示样本数量。

   权重导数

   损失函数相对于权重的导数可写为：
   $$\frac{\partial }{\partial w} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2$$
   

   并计算出以下结果：
   $$\frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2x_{(i)}$$

   首先，我们将每个预测值减去实际值，然后将其乘以特征值的两倍。 然后，我们将总和除以示例数量。 结果是与权重值相切的直线的斜率。

   如果我们求解此方程，并将权重和偏差设为零，则会得到 -119.7 的直线斜率。

   偏差导数

   损失函数相对于偏差的导数可写为：
   $$\frac{\partial }{\partial b} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2$$
   

   并计算得出：
   $$\frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2$$

   首先，我们计算每个预测值与实际值之差的总和，然后将该总和乘以 2。然后，我们将总和除以样本数量。结果是与偏差值相切的直线的斜率。

   如果我们求解此方程，并将权重和偏差设为零，则会得到 -34.3 的直线斜率。

4. 沿负斜率方向移动少量距离，即可得到下一个权重和偏差。目前，我们将任意定义“少量”为 0.01：$$Newweight=oldweight-(smallamount\ast weightslope)$$$$Newbias=oldbias-(smallamount\ast biasslope)$$$$Newweight=0-(0.01)\ast (-119.7)$$$$Newbias=0-(0.01)\ast (-34.3)$$$$Newweight=1.2$$$$Newbias=0.34$$

使用新的权重和偏差计算损失并重复此过程。完成六次迭代后，我们将获得以下权重、偏差和损失：

迭代	重量	偏见	损失（均方误差）
1	0	0	303.71
2	1.20	0.34	170.84
3	2.05	0.59	103.17
4	2.66	0.78	68.70
5	3.09	0.91	51.13
6	3.40	1.01	42.17

您可以看到，随着每次更新权重和偏差，损失会越来越小。 在此示例中，我们在六次迭代后停止了训练。实际上，模型会一直训练，直到收敛为止。 当模型收敛时，额外的迭代不会进一步减少损失，因为梯度下降法已经找到了几乎可将损失降至最低的权重和偏差。

如果模型在收敛后继续训练，损失会开始小幅波动，因为模型会不断更新参数，使其接近最低值。这可能会导致难以验证模型是否已实际收敛。如需确认模型是否已收敛，您需要继续训练，直到损失趋于稳定。

模型收敛和损失曲线

训练模型时，您通常会查看损失曲线，以确定模型是否已收敛。损失曲线显示了损失随模型训练的变化情况。下图显示了典型的损失曲线。损失位于 y 轴上，迭代次数位于 x 轴上：

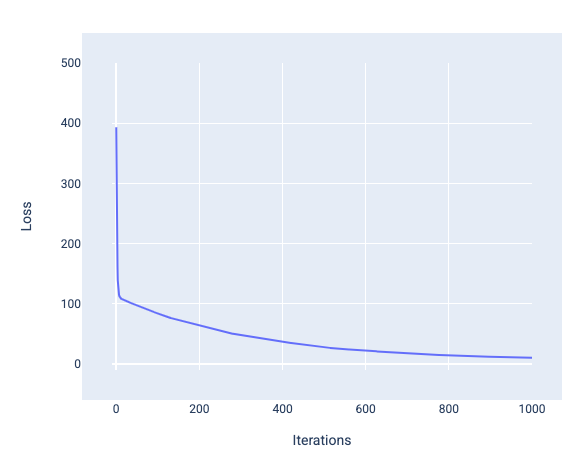
图 12. 损失曲线，显示模型在第 1,000 次迭代左右收敛。

您可以看到，在前几次迭代中，损失大幅减少，然后逐渐减少，在第 1,000 次迭代左右趋于平缓。经过 1,000 次迭代后，我们基本上可以确定模型已收敛。

在下图中，我们绘制了模型在训练过程中的三个时间点（开始、中间和结束）的状态。直观呈现训练过程中各个时间点的模型状态，有助于巩固权重和偏差更新、损失减少与模型收敛之间的关联。

在图中，我们使用特定迭代次数时得出的权重和偏差来表示模型。在包含数据点和模型快照的图中，从模型到数据点的蓝色损失线表示损失量。线条越长，损失越大。

在下图中，我们可以看到，在第二次迭代左右，由于损失过大，模型将无法很好地进行预测。

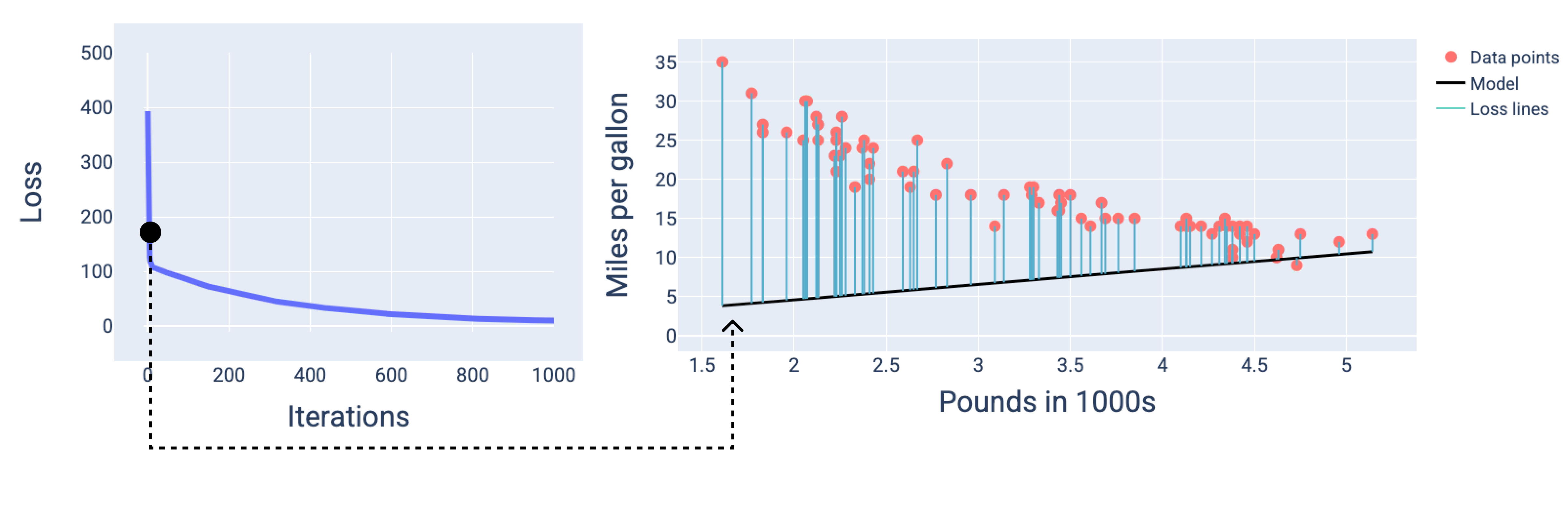
图 13. 训练过程开始时的损失曲线和模型快照。

在大约第 400 次迭代时，我们可以看到梯度下降已经找到了能够生成更好模型的权重和偏差。

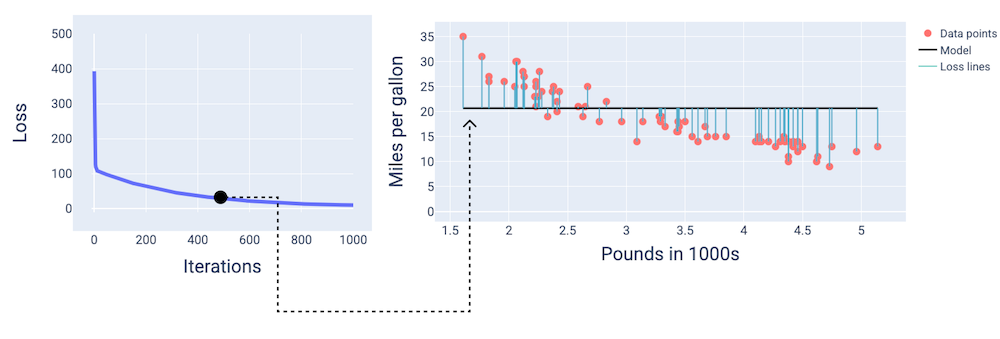
图 14. 损失曲线和训练中途的模型快照。

在大约第 1,000 次迭代时，我们可以看到模型已收敛，生成了损失尽可能最低的模型。

图 15. 损失曲线和训练过程接近结束时模型的快照。

练习：检查您的理解情况

梯度下降在线性回归中的作用是什么？

• 梯度下降法是一种迭代过程，用于找到可最大限度减少损失的最佳权重和偏差。
• 梯度下降有助于确定在训练模型时使用哪种类型的损失，例如 L₁ 或 L₂。 (梯度下降不涉及模型训练的损失函数选择。)
• 梯度下降会从数据集中移除离群值，以帮助模型做出更好的预测。(梯度下降不会更改数据集。)

收敛和凸函数

线性模型的损失函数始终会生成凸面。根据这一属性，当线性回归模型收敛时，我们知道该模型已找到可产生最低损失的权重和偏差。

如果我们绘制具有一个特征的模型的损失曲面图，可以看到其凸形。下图显示了假设的每加仑英里数数据集的损失曲面。权重位于 x 轴上，偏差位于 y 轴上，损失位于 z 轴上：

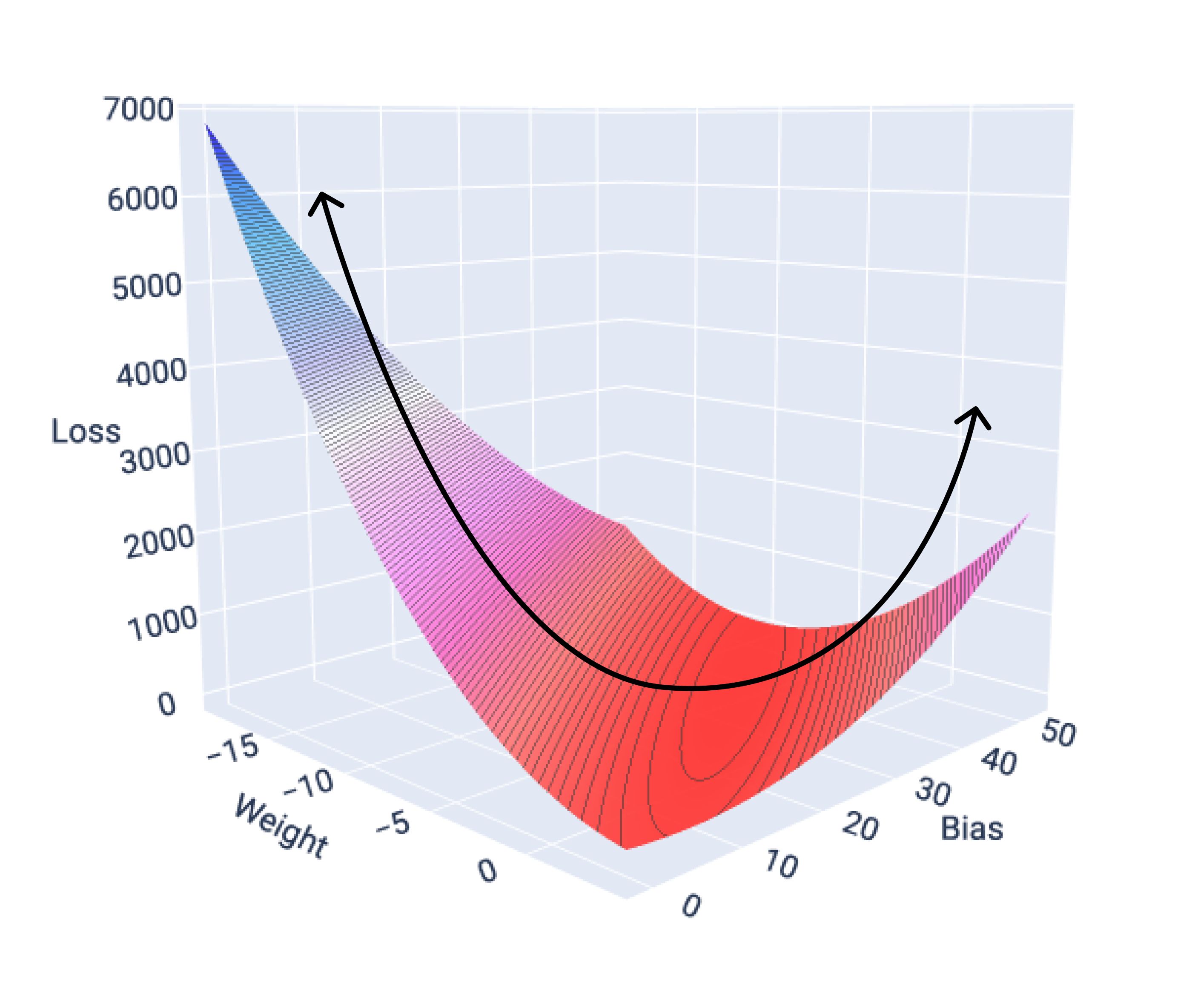
图 16. 显示凸形的损失曲面。

在此示例中，权重为 -5.44，偏差为 35.94，可产生最低的损失（5.54）：

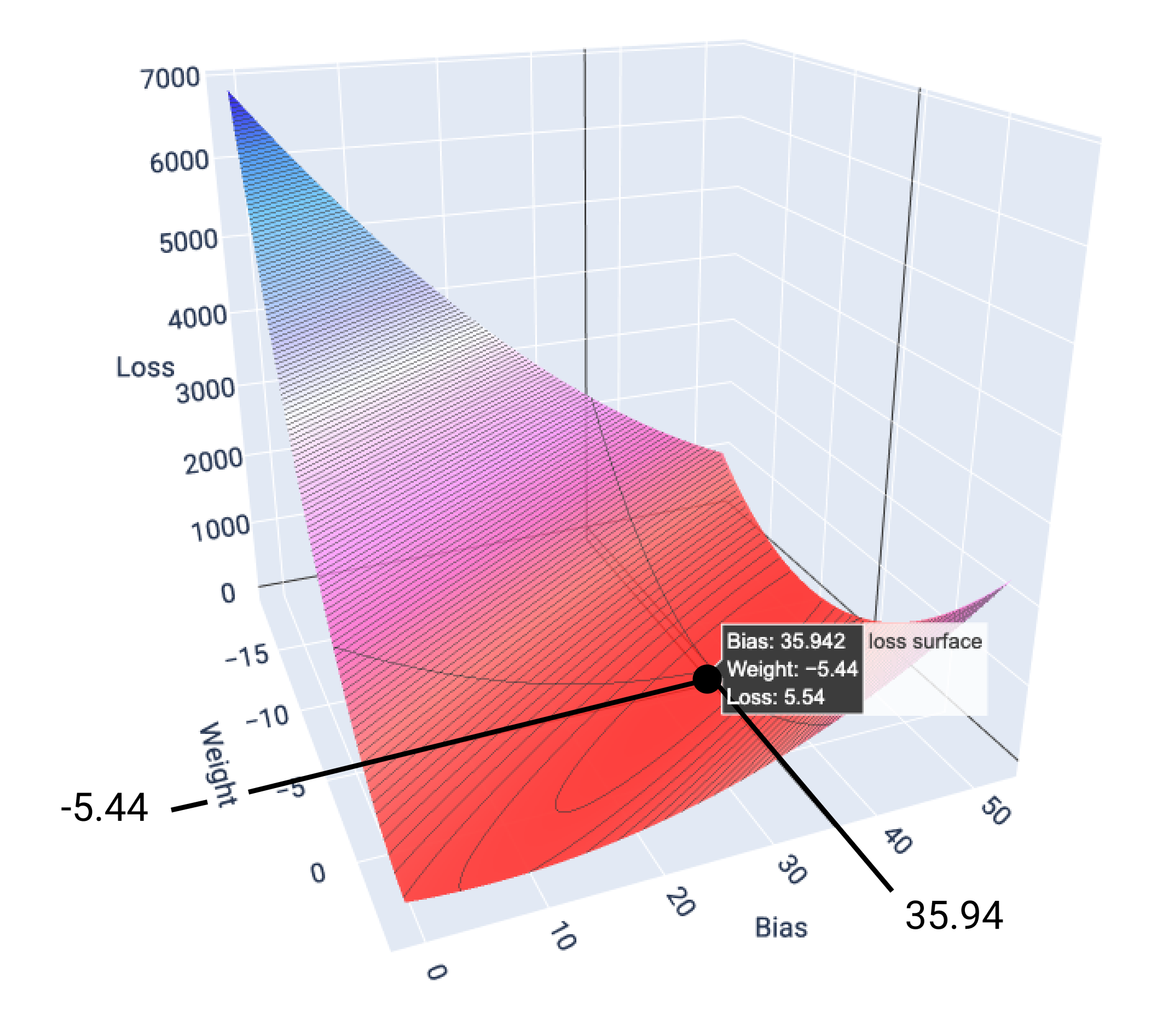
图 17. 显示产生最低损失的权重和偏差值的损失面。

当线性模型找到最小损失时，它会收敛。因此，额外的迭代只会导致梯度下降在最小值附近以非常小的幅度移动权重和偏差值。如果我们绘制梯度下降期间的权重和偏差点，这些点看起来就像一个球从山上滚下来，最终停在没有更多向下坡度的点。

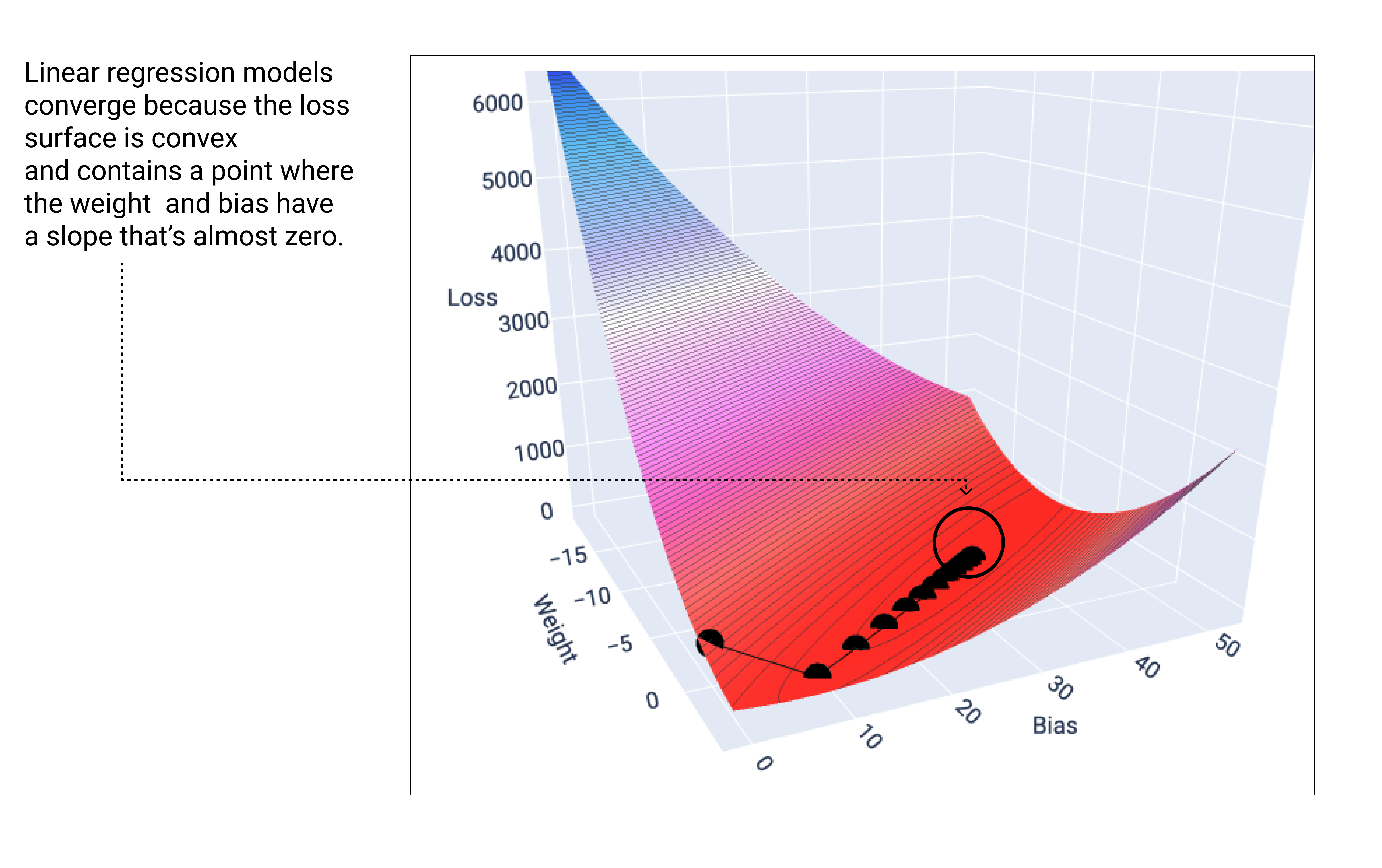
图 18. 损失图，显示了梯度下降点停止在图表最低点的情况。

请注意，黑色损失点会形成损失曲线的确切形状：先是急剧下降，然后逐渐向下倾斜，直到达到损失曲面上的最低点。

请务必注意，模型几乎不会找到每个权重和偏差的精确最小值，而是会找到非常接近该最小值的值。另请务必注意，权重和偏差的最小值并不对应于零损失，而只是能为相应参数产生最低损失的值。

使用产生最低损失的权重和偏差值（在本例中，权重为 -5.44，偏差为 35.94），我们可以绘制模型图，看看它与数据的拟合程度如何：

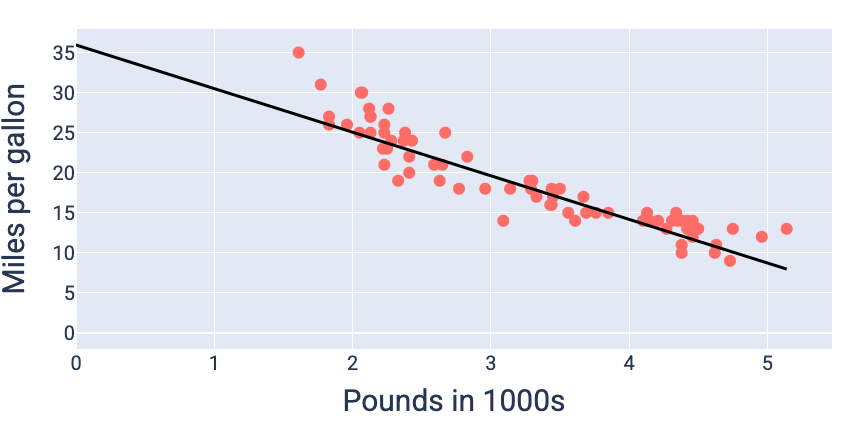
图 19. 使用产生最低损失的权重和偏差值绘制的模型图。

对于此数据集，这将是最佳模型，因为没有其他权重和偏差值能生成损失更低的模型。

**关键术语**

• Convergence
• 凸函数
• 梯度下降法
• 迭代
• 损失曲线

线性回归：超参数

超参数是控制训练不同方面的变量。以下是三种常见的超参数：

• 学习速率
• 批次大小
• 周期

相比之下，形参是模型本身的一部分，例如权重和偏差。换句话说，超参数是您控制的值；参数是模型在训练期间计算的值。

学习速率

学习速率是一个您设置的浮点数，用于影响模型收敛的速度。如果学习率过低，模型可能需要很长时间才能收敛。不过，如果学习速率过高，模型将永远无法收敛，而是在可最大限度减少损失的权重和偏差附近跳动。目标是选择一个既不太高也不太低的学习速率，以便模型快速收敛。

学习速率决定了在梯度下降过程的每一步中，对权重和偏差所做的更改幅度。模型将梯度乘以学习速率，以确定下一次迭代的模型参数（权重和偏差值）。在梯度下降的第三步中，沿负斜率方向移动的“少量”是指学习速率。

旧模型参数与新模型参数之间的差异与损失函数的斜率成正比。例如，如果斜率较大，模型会采取较大的步长。如果较小，则采取较小的步长。例如，如果梯度的大小为 2.5，学习率为 0.01，则模型会将形参更改 0.025。

理想的学习率有助于模型在合理的迭代次数内收敛。在图 20 中，损失曲线显示模型在前 20 次迭代中显著改进，然后开始收敛：

图 20. 损失图，显示了以可快速收敛的学习速率训练的模型。

相比之下，如果学习速率过小，则可能需要过多的迭代次数才能实现收敛。在图 21 中，损失曲线显示模型在每次迭代后仅略有改进：

图 21. 损失图，显示了以较小学习速率训练的模型。

过大的学习速率永远不会收敛，因为每次迭代都会导致损失在较大范围内波动或持续增加。在图 22 中，损失曲线显示模型在每次迭代后损失先减少后增加；在图 23 中，损失在后续迭代中增加：

图 22. 损失图，显示了以过大的学习速率训练的模型，其中损失曲线随着迭代次数的增加而剧烈波动，时而上升时而下降。

图 23. 损失图，显示了以过大的学习速率训练的模型，其中损失曲线在后来的迭代中急剧增加。

练习：检查您的理解情况

理想的学习率是多少？

• 理想的学习速率取决于具体问题。
• 0.01
• 1.0

说明： 每个模型和数据集都有自己的理想学习率。

批次大小

批次大小是一种超参数，指的是模型在更新权重和偏差之前处理的示例数量。您可能会认为，模型应先计算数据集中每个样本的损失，然后再更新权重和偏差。不过，如果数据集包含数十万甚至数百万个示例，则使用完整批次并不实际。

以下两种常见技术可在不查看数据集中的每个示例的情况下，获得正确的平均梯度，然后更新权重和偏差：随机梯度下降和小批量随机梯度下降。

• 随机梯度下降法 (SGD)：随机梯度下降法在每次迭代中仅使用一个示例（批次大小为 1）。在迭代次数足够多的情况下，SGD 可以正常运行，但噪声非常大。“噪声”是指训练期间导致损失在迭代过程中增加而非减少的变化。“随机”一词表示每个批次中的一个示例是随机选择的。

  请注意，在下图中，当模型使用 SGD 更新权重和偏差时，损失会略有波动，这可能会导致损失图出现噪声：

  

  图 24. 使用随机梯度下降法 (SGD) 训练的模型，显示损失曲线中的噪声。

  请注意，使用随机梯度下降可能会在整个损失曲线中产生噪声，而不仅仅是在接近收敛时。

• 小批次随机梯度下降法（小批次 SGD）：小批次随机梯度下降法是全批次和 SGD 之间的折衷方案。对于 $N$ 个数据点，批次大小可以是大于 1 且小于 $N$ 的任意数字。模型会随机选择每个批次中包含的示例，对它们的梯度求平均值，然后在每次迭代中更新一次权重和偏差。

  确定每个批次的样本数量取决于数据集和可用的计算资源。一般来说，小批量大小的行为类似于 SGD，而大批量大小的行为类似于全批量梯度下降。

  

  图 25. 使用小批次随机梯度下降法训练的模型。

在训练模型时，您可能会认为噪声是一种应消除的不良特征。不过，一定程度的噪音可能是一件好事。在后续模块中，您将了解噪声如何帮助模型更好地泛化，以及如何在神经网络中找到最佳权重和偏差。

周期数

在训练期间，一个周期是指模型已处理训练集中的每个示例一次。例如，如果训练集包含 1,000 个示例，而小批次大小为 100 个示例，则模型需要 10 次迭代才能完成一个周期。

训练通常需要多个周期。也就是说，系统需要多次处理训练集中的每个示例。

周期数是一种超参数，您需要在模型开始训练之前设置该参数。在许多情况下，您需要通过实验来确定模型收敛所需的周期数。一般来说，训练周期数越多，模型效果越好，但训练时间也越长。

图 26. 完整批次与小批次。

下表介绍了批次大小和周期与模型更新其参数的次数之间的关系。

批次类型	权重和偏差更新何时发生
完整批次	模型查看完数据集中的所有示例后。例如，如果某个数据集包含 1,000 个样本，并且模型训练了 20 个周期，则模型会更新权重和偏差 20 次，每个周期更新一次。
随机梯度下降法	模型查看数据集中的单个示例后。 例如，如果某个数据集包含 1,000 个样本，并且训练了 20 个周期，则模型会更新权重和偏差 20,000 次。
小批次随机梯度下降法	模型查看完每个批次中的示例后。例如，如果某个数据集包含 1,000 个样本，批次大小为 100，并且模型训练了 20 个周期，则模型会更新权重和偏差 200 次。

练习：检查您的理解情况

1. 使用小批次随机梯度下降法时，最佳批次大小是多少？

   • 视情况而定
   • 每个批次 10 个示例
   • 每个批次 100 个示例

   说明： 理想的批次大小取决于数据集和可用的计算资源。

2. 以下哪项陈述是正确的？

   • 较大的批次不适合包含许多异常值的数据。
   • 将学习速率提高一倍可能会减慢训练速度。

   说明： 将学习速率加倍可能会导致学习速率过大，从而导致权重“四处波动”，增加收敛所需的时间。与往常一样，最佳超参数取决于您的数据集和可用的计算资源。

**关键术语**

• 批次大小
• Epoch
• 广义化
• 超参数
• 迭代
• 学习率
• 小批次
• 小批次随机梯度下降法
• 神经网络
• 参数
• 随机梯度下降法